How Simshady Works

Simshady models the yield of photovoltaic (PV) systems by considering two primary factors: weather/climate data and shading from local 3D geometry.

3D Scene Setup

PV system output is heavily influenced by shading from nearby objects—such as buildings, vegetation, or terrain. Simshady represents this environment through a ShadingScene, which is composed of three.js geometries.

• Use addMainGeometry() to define the primary object for simulation (e.g., PV panels or the target building).
• Use addShadingGeometry() to add surrounding objects that may cast shadows (e.g., neighboring buildings, trees).

Weather, Climate, and Skydomes

Simshady uses time-series data of Global Horizontal Irradiance (GHI) and Direct Normal Irradiance (DNI) from NREL for locations in Germany. These datasets do not include directional irradiance information, so Simshady reconstructs it using the HEALPix framework, which divides the sky dome into 96 equal-area segments.

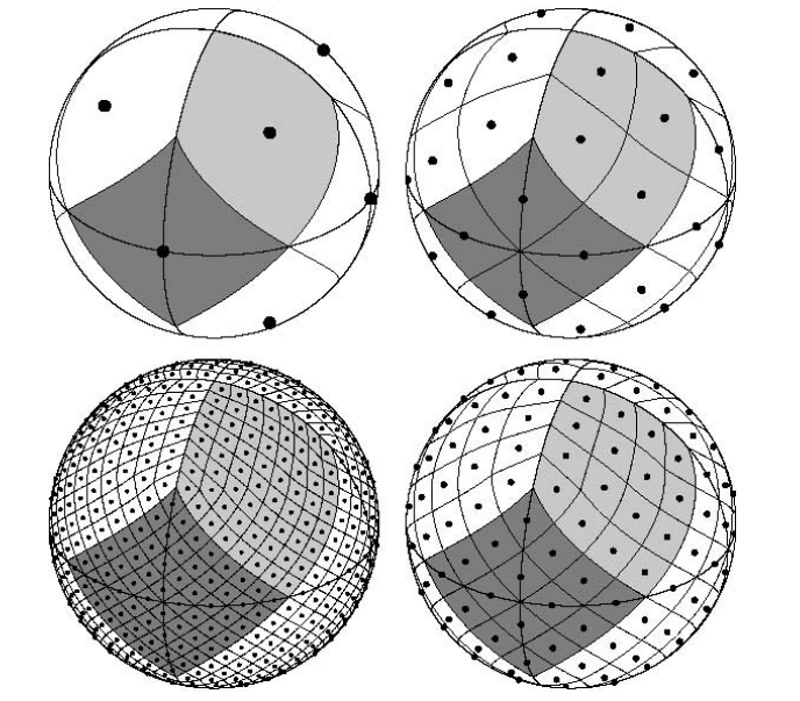
Figure 1: Sky discretization using HEALPix, from Gorski et al.

For each time step:

• DNI is assigned to the sky segment corresponding to the sun's position.
• The diffuse component (GHI - DNI) is distributed equally across all sky segments, weighted by the sine of the solar altitude angle.

The resulting irradiance on a flat surface is:

Irradiance = DNI × sin(altitude) + Σ(Diffuse_segment × sin(altitude))
Copy

Why Skydomes?

There are two key reasons for using skydomes:

1. They enable simultaneous simulation of direct and diffuse solar radiation.
2. They allow for time-resolved PV yield simulation.

The process works as follows:

1. For each sky segment and each triangle of the simulation geometry, Simshady uses the Möller-Trumbore algorithm to check if the line of sight is obstructed by any shading geometry. The result is:

   • 0 if an intersection occurs.
   • The dot product between the triangle normal and the vector to the sky segment if unshaded.

   This produces a shading mask of shape S x N, where S is the number of sky segments and N is the number of triangles. Each value is between 0 and 1.

2. Radiance values from the sky dome are integrated over time. If irradiance data is provided as a time series with shape S x T (S = sky segments, T = time steps), the energy received by triangle n at time t is:

E(t, n) = 1 / (2 × π) × Σ(Mask(s, n) × irrad(s, t))
Copy

The result E(t, n) is the irradiance in Wh/m².

GPU-Accelerated Simulation

Since the computation for each triangle is independent, the simulation is fully parallelizable. The Möller-Trumbore intersection algorithm is implemented in WebGL to leverage GPU acceleration, enabling efficient real-time simulation of shading and solar irradiance.